The universe’s storehouse of energy
According to the recently deceased Arthur C. Clarke (1999, p. 495), Richard Feynman’s appraisal regarding zero point energy (ZPE) was that a cubic meter of space would have enough energy to boil all the Earth’s oceans.
By “boiling the earth’s oceans” we are here going to assume that the vaporization is done at uniform 1 atmosphere pressure. Obviously, in a real planet, as an ocean boils away into the atmosphere, it would thicken the atmosphere and hence increase the pressure, making the calculation far more complicated. (It would also escalate the planetary temperature, a la Venus’ runaway greenhouse effect, hence requiring less external input of enthalpy to finish the vaporization process). I imagine that Arthur Clarke wouldn’t have gone to this trouble when he ventured his rough estimate, which he attributed to another scientist (Feynman) anyway.
With this simplifying assumption, the ZPE density adduced by Clarke translates to ~3×1027 J/m3. To put this figure into perspective:
§ The energy released in the combustion of one cubic meter of say, petrol (gas in the U.S.) is ~4×1010 J. This is a typical chemical energy release.
§ The energy released in the fission of one cubic meter of U-238, the most common uranium isotope, in a breeder reactor (in which all the natural U-238 is induced by neutrons to become fissionable), is ~1.5×1018 J. This would be a typical nuclear energy release. The energy given off in the thermonuclear D-D fusion from the deuterium naturally present in a cubic meter of water (say, seawater), would be ~8×1012 J. Fusion is more powerful than fission per unit of fuel mass, but in nature only 0,015% of hydrogen atoms are deuterium (Hubbert, 1971, p. 38).
§ The energy released in the hypothetical complete annihilation of the subatomic particles of half a cubic meter of seawater with their corresponding antiparticles, would be ~1020 J. This is the theoretical maximum amount of energy that can be extracted from mass, with Einstein’s E=mc2 utilized at its full 100%.
This is to say, according to Feynman the vacuum has well over ten million times the maximum energy that can be extracted from the complete annihilation of the mass of a typical natural substance such as water.
Clarke’s quotation might be a slight misprint, and possibly the original calculation to which our missed science-fiction luminary was referring to was one, attributed to John Wheeler, by which the energy of the vacuum in a teacup (not in a cubic meter) would be what would make the Earth’s oceans boil. If so, the potential quarry of the universe’s ZPE would be upped to 1030 J/m3. R. Podolny in 1986 went even further to 1050 J/m3. Not in vain, ZPE has been described as the ultimate free lunch even by mainstream science journalists (Seife, 1997).
Now, the opinion of Harold E. Puthoff and most active researchers in this field is based on Sakharov’s studies and the arguments of Feynman and Hibbs. In this line of thinking, the vacuum spectral energy density distribution is given by (Haisch, Rueda and Puthoff, 1994; Beck and Mackey, 2008):
![]() ħ
ħ
, where w is the frequency of each mode of electromagnetic radiation, ħ is (the small) Planck’s constant, and c is the speed of light. The integrated energy density from frequency wi to frequency wf is then:
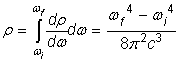 ħ
ħ
It is obvious that if we integrate this energy density spectrum for the full range of frequencies w possible, from 0 to infinity, the resulting energy density of the vacuum r diverges up to infinity. Many physicists postulate that this is absurd, and contend therefore that a cutoff frequency wc must exist. The natural cutoff, it is argued, must then be Planck’s frequency:
ωPlanck = (c5/ħG)1/2 = 1.9 × 1043 s-1
, where G is Newton’s universal constant of gravitation. The rationale is that at Planck’s frequency, space-time becomes foamy and the standard model of Physics breaks down, the description of nature necessitating the still undeveloped theories of quantum gravity or superstrings. Hence it makes no sense to extrapolate the electromagnetic normal modes description of the vacuum beyond this frequency.
With this cutoff, the total vacuum energy density becomes:
 ħ =
ħ = ![]() ħ-1
ħ-1
, this is to say, ~4×10112 J/m3!
Robert Forward and Moray King, however, don’t think that the energy contributions of the electromagnetic normal modes should stop at Planck’s frequency, and hence venture that the theoretical available energy density of the vacuum could indeed be infinite!
Beck, Christian and Mackey, Michael C., “Could dark energy be measured in the lab?”, dated February 2, 2008, as accessed on arxiv.org/PS_cache/a…
Clarke, Arthur C., “Greetings, Carbon-based bipeds”, Voyager, HarperCollins Publishers, London, 1999.
Haisch, B.; Rueda, A. and Puthoff, H.E., “Inertia as a zero-point-field Lorentz force”, Phys. Rev. AVol. 49, Number 2, 678-694, February 1994.
Hubbert, M. King, “The energy resources of the Earth”, in Energy and Power, a Scientific American book. 1971, www.hubbertpeak.com/…
Seife, Charles, “Quantum Mechanics: The Subtle Pull of Emptiness”, Science Vol. 275, #5297, pp. 158, January 10, 1997
For more information on Conrado’s Work see: www.newenergytimes.c…

