By Fredrik Nygaard fredrik_nygaard@hotm…
September 28 2015, Porto Portugal.
Also see Fredrik’s Websiite: www.universeofpartic…
Introduction
As an electrical engineer with a life long interest in science, I was intrigued to discover Peter Woodhead’s two papers and videos on his proposed mechanism for how the earth may have expanded from the time of the dinosaurs, and how gravity as measured on the surface of our planet could have increased in the process.
Unlike most people who have put forward theories in order to explain and defend the expanding earth theory, Peter Woodhead does not call for any increase in mass. Instead, he postulates that the expansion has been due to internal pressures, primarily from water turning to steam, and that surface gravity has increased due to a process where the heavy stuff of our planet has risen up towards the surface.
There are two advantages to this theory compared to theories involving an increase in mass. One being that we do not have to invent a mechanism in which mass is increased or absorbed by our planet. And the other being that we do not have to explain why our moon has not crashed into our planet due to the extra gravitational pull caused by the increase in mass.
Woodhead’s postulations imply that the change in gravity experienced at the surface of our planet do not affected the overall gravitational pull of our planet on distant object such as the sun and the moon.
And with no known mechanism to explain an increasing mass of our planet, Woodhead’s theory comes across as both clean and elegant, requiring nothing new or unknown to explain the change in surface gravity. However, critics have been quick to raise two objections that have to be addressed before they are willing to consider his theory as viable.
The first objection is the fact that Peter Woodhead’s theory violates Newton’s Shell Theorem which states that a gravitational body can always be modeled as having all of its mass located at its geometrical center. An expanding earth with no added mass would therefore result in a reduced surface gravity regardless of where the heavy stuff of our planet is located.
The second objection has to do with liquids and gases. At the pressures presumed to exist at the center of our planet, it is simply impossible to produce gases from liquids, and it follows that a steam powered expansion cannot happen.
However, both of the above objections presume gravity to be a point source at the atomic level. For a model of gravity, such as the one developed by the Electric Universe community, where the atomic unit of gravity is a dipole rather than a point source, the Shell Theorem does not apply, and the pressure at the center of our planet cannot be presumed to be particularly high.
Newton’s Shell Theorem
An important but frequently overlooked premise for Newton’s Shell Theorem is that every atomic unit involved in the calculation must be a point source acting with equal force in all directions. If this is not the case, the Shell Theorem cannot be used to simplify things.
If the atomic unit of force is a dipole, as is the case in the Electric Universe model, the Shell Theorem simply does not apply.
In fact, for any model in which the atomic unit of gravity is a dipole, surface gravity is determined entirely by how heavy and light elements are distributed.
If, as Peter Woodhead postulates, heavy matter has risen and become concentrated close to the surface of our planet, then surface gravity must have increased in the process.
Center of Gravity, Using the Electric Universe Model
While the center of gravity in the standard model is located at the geometrical center of our planet, it can be shown that this is not the case for the Electric Universe model.
The Electric Universe model will in fact place the center of gravity at a considerable distance away from the geometrical center.
For the Electric Universe model, gravity can be modeled at the atomic level as "gravitational stick magnets", and surface gravity is simply the result of all these "gravitational stick magnets" lining up with their plus poles facing in towards the center of our planet and their minus poles facing out towards the surface.
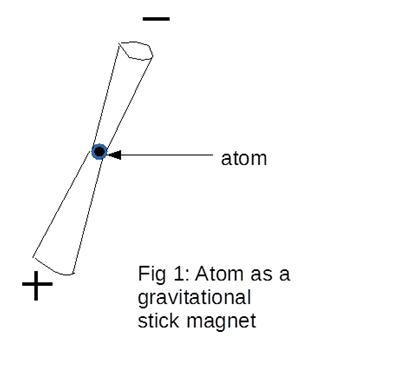
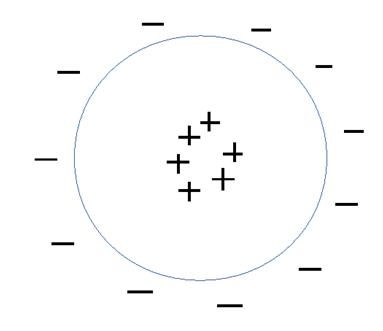
Fig 2. Earth as a gravitational charged body
Note that the "gravitational stick magnets" meet with their positive poles at the center of our planet. And from this we can conclude that there is "gravitational pressure" in addition to any other pressures, such as steam, inside our planet.
It can also be concluded that the "gravitational stick magnets" at the far side of our planet do not positively add to the gravity felt on our side of the planet.
Furthermore, an observer moving in towards the center of our planet will at some point reach a place where the overall gravitational pull goes from negative to positive. At that point the observer will experience weightlessness before again regaining weight on his or her way towards the geometrical center.
Note that the observer will never experience gravity to be repelling as his or her internal "stick magnets" will always be oriented with plus facing towards the geometrical center of our planet. What changes is the direction that the observer has to exert force in order to move further towards the geometrical center.
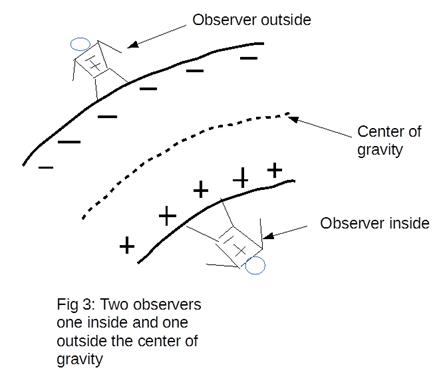
The center of gravity is the place where the overall gravitational pull changes direction, and for any model that does not give the far hemisphere the same weight as the near hemisphere, the center of gravity must necessarily lay away from the geometrical center.
In the Electric Universe model, the far hemisphere does in fact exercise a repelling force on the near hemisphere, so it is clear that the center of gravity for this model does not reside in the geometrical center of our planet.
And since the center of gravity is located where gravity pulls equally in all direction, the center of gravity must also be a place of zero net gravitational pull.
So while the standard model predicts zero gravity only at the center of our planet, the Electric Universe models predicts zero gravity at the center of gravity due to gravitational symmetry, and again at the center of our planet due to geometrical symmetry.
Note that if the core of our planet is full of light stuff (= week stick magnets), then the center of gravity will lay closer to the surface where the heavy stuff (= strong stick magnets) are located. Conversely, if the core is full of heavy stuff, the center of gravity will lay closer to the center.
And it follows from this that for the Electric Universe model, a steam powered expansion of our planet will result in the center of gravity moving out towards the surface. However, since such an expansion will make the non-gaseous shell thinner, it does not necessarily follow that the surface gravity will increase as a consequence.
Surface gravity is not merely a question of where the center of gravity is located, but also a question of how thick the non-gaseous shell is.
However, before we go on to locate the center of gravity and what effect this has for surface gravity, we should first address the second objection to Peter Woodhead’s theory.
Internal Pressures
When it comes to liquids turning into gas, it is true that temperature in itself cannot make this happen, and liquids simply do not turn to gas if pressure is above a certain level.
It has been shown that water at a depth of only 2 km beneath the surface of the earth’s crust do not turn into gas at any temperature due to the pressures at this depth, and proposing that the gas inside our planet may be nitrogen, rather than water, does nothing to solve this problem. And the pressures at the center of our planet, according to the standard model of gravity, are so high that nothing would turn to gas.
However, using the Electric Universe model instead of the standard model we get quite a different picture.
What we have to keep in mind for the Electric Universe model is that "down" is always in the direction of the center of gravity, and this means that "down" is towards the surface of our planet for anything close to the geometrical center of our planet, as illustrated in Fig 3.
It is clear, therefore, that a cavity located at the geometrical center of our planet will experience pressure only from the gases and vapors located inside of it, since all the heavy stuff, like liquids and solids, will exert pressure only in the direction of the center of gravity.
An interesting consequence of this is that a cavity, once formed at the center of our planet, will tend to grow and never shrink. Heavy stuff will be continuously pushing towards the center of gravity. Cracks and openings on the inside surface will see heavy stuff like rocks and liquids slip into them while vapors and gasses will move "up" towards the geometrical center of our planet.
This process will be continuous and erosive, so even if the effect of a cavity at the center of a young planet may hardly be noticeable, the crust of the planet will sooner or later crack under the relentless pressure, triggering expansion. And once expansion has started it will not stop before the process finally exhausts itself.
Locating the Center of Gravity, Using Volumes of Spheres
Having dealt with the two main objections to Peter Woodhead’s theory, we can go on to make calculations and predictions based on the Electric Universe model, as it applies to an expanding planet.
To find out where the center of gravity of our planet is presently located, assuming that our planet has expanded, we can best start by considering where the center of gravity must have been before the expansion process started.
To do this, we start by making the assumption that our planet was solid all the way through to start with and that the heavy and light stuff was distributed evenly throughout.
From this we get that the center of gravity must have been located where there was an equal volume of matter on either side of it.
Letting Vtotal be the total volume of the pre-expansion planet and Vcg be the volume enclosed by its center of gravity we get:
![]()
Using the equation for volume of a sphere we get:
![]()
Removing constants on both side of the equation:
![]()
Letting Rcg = 1 to establish the relationship Rtotal/Rcg
Rtotal3 = 2
Rtotal/Rcg = 1.26
The distance to the center of gravity from the geometrical center of our planet was in other words about four times bigger than the distance from the center of gravity to the surface.
So, if the radius of the pre-expansion earth was 3763 km, its center of gravity was located about 750 km below the surface.
Using the same logic, we can find the current location of the center of gravity by assuming that it must have equal volume of non-gaseous elements on either side of it.
With the earth’s radius today being 6370 km, the non-gaseous shell is only 470 km thick, which has as a consequence that the outer perimeter of the non-gaseous shell is not very much bigger than the inner perimeter, and it follows that the center of gravity will be located only marginally closer to the outer perimeter as to its inner perimeter in order to have equal volumes of stuff inside and outside of it.
Without doing any calculations, we can estimate the center of gravity to be currently located at roughly 220 km below the surface.
In other words, using purely geometric considerations, we can conclude that the center of gravity was located at roughly 750 km below the surface pre-expansion, and is currently located at roughly 220 km below the surface.
Calculating Changes in Strength of the Center of Gravity Due to Expansion
Having located the center of gravity for both the pre-expansion and the current expansion case, we must go on to consider the gravitational strength of these two center’s of gravity before we can say anything about gravity as experienced at the surface of our planet.
We cannot merely compare the two locations, as the gravitational pull exerted by the two centers of gravity are not the same.
We have to figure out the relative strength of the two centers of gravity. And only when we have both the location and the strength of each center of gravity can we compare the two cases in order to find out how surface gravity has changed with our planet’s expansion.
Since gravity is a property of mass, the way we figure out the strength of the center of gravity is to consider the mass represented by each point on its surface. For each point of the center of gravity, we can say that the mass that it represents is directly proportional to the depth of the non-gaseous shell. The strength S of the center of gravity equals the depth of the non-gaseous shell D, multiplied by a constant K.
S = K x D
From this we get:
Spre = K x 3763 km
and
Snow = K x 470 km
And from this we see that the strength of Spre relative to Snow is pretty much exactly 8 to 1:
Spre / Snow = 3763 / 470 = 8
Calculating Changes in Surface Gravity Due to Expansion
Now that we have a figure for the relative strength of the center of gravity as it has changed from pre-expansion to current expansion in addition to the location of the two centers of gravity, we can calculate how surface gravity has changed.
To do this we have to keep in mind that we are dealing with dipoles which follow the inverse cube law, and not the inverse square law used by Newton. The correct function for this purpose is therefore not
![]()
but
![]()
where K is some unknown constant similar to Newton’s Gravitational Constant.
Replacing M1 with S we get:
![]()
And to get the relationship between pre-expansion surface gravity and current surface gravity we get the following:
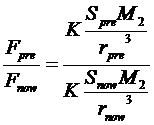
Which simplifies to:
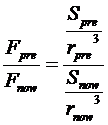
And, plugging in the numbers we get:

Which represents a 500 per cent increase in surface gravity since pre-expansion.
Our calculations give us in other words an increase in surface gravity that is in good agreement with that seen in relation to the estimated increase in surface gravity of about 400 per cent made based on analysis of fossil records.
However, a troubling problem remains, namely the fact that gravity does not taper off at anything remotely like the inverse cube law for an observing moving to higher elevations.
Changes in Gravity with Changes in Altitude
Having established that the inverse cube law fits well with surface gravity as it applies to a growing earth, we have to deal with the fact that our findings do not seem to fit observed changes in gravity relative to altitude.
Going up 10 km in a plane results in a change in gravity of about 1 per cent. However, were we to use the inverse cube law with a distance to the center of gravity from the surface of 220 km, the change would calculate to about 12.5 per cent:
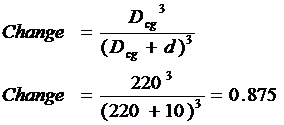
And it is clear that the inverse cube law cannot be used without some modifying factor. However, this is not a problem since there is a rather obvious moderating effect that we need to consider anyway, namely the effect of altitude itself.
First of all, it seems reasonable to assume that gravity spreads in a very different manner inside the hard shell of our planet than outside of it. Just like we can envision magnetic force fields being highly directional inside a magnet, we can expect gravity fields to be highly directional with little or no spread inside the crust of our planet.
However, once gravity fields leave the crust of our planet, they are likely to spreads out in a similar manner to that of magnetic fields. And the effect of this is that an observer at an altitude of 10 km will have a lot more gravity fields reaching him than an observer at ground level.
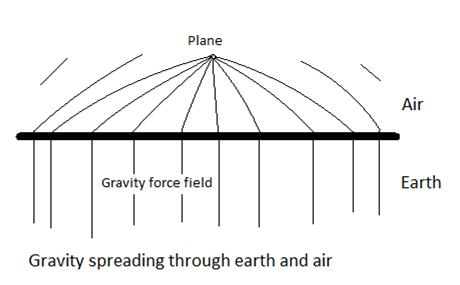
Fig 4
So while the force of gravity tapers off at the inverse cube law, the observer is affected by a gravitational disk reaching for him from the surface.
The moderating effect is in other words some variation on the equation for the area of a disk, and the moderating factor Mod(d) can be expressed as follows:
Mod(d) = P(d) x p x d2
where P(d) is some unknown function of an observer’s distance to the surface of our planet, expressing the extent to which the gravitational field fans out with distance.
A reasonable range for P(d) would be between 1 and 5 for observers located relatively close to the surface, indicating a fan out from one to five times the altitude of the observer.
If P(d) is 1, the radius of the area moderating the final result is equal to the height of the observer above ground. If P(d) = 5, the radius of the disc pulling the observer down is 5 times greater than the height of the observer from the ground.
Keeping in mind that the moderating factor only applies to the distance of an observer above the surface of our planet, we have to make sure we use it in a way that reflects the fact that Mod(d) varies with d2 while Change in gravity alone varies with d3.
This means that the distance d above ground has to be replaced by a function of d f(d) in the Change function.
Instead of:
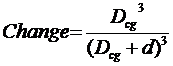
we get:
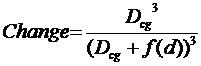
where f(d) is the moderated effect of the distance from the surface to the observer.
Using

we get:
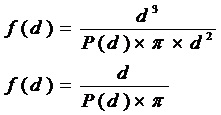
So when we put f(d) into the Change function we get:
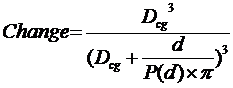
And since we know from experiment that Change = 1 per cent at 10 km, we find that P(10km) = 5 gives us the correct answer.
If we set P(d) = 5, indicating a disc with a radius 5 times bigger than the observer’s altitude, we get:
Change = 2203/(220 + 10/15.7)3 = 0.991
Hence, this is very close to a 1% change. In other words, if the center of gravity of our planet is located at 220 km below the surface, the gravitational field must spread outwards in all directions in such a way that gravity five times as distant as a plane’s cruising altitude of 10 km has a significant influence on the gravitational pull on the plane and its occupants.
The disc of gravitational influence on an observer at 10 km altitude must have an extent of about 50 km in all directions. And since we can assume that gravity fans out from the surface of our planet in a similar way to that of a magnet, we can assume the fanning out to be considerable less than 5 at ground level:
P(0) < 5
In other words, we can assume the fan out to be a mere P(0) = 1 or less on the ground level. The disk of gravitational fields pulling on us at ground level may be as little as a mere meter around us on either side.
In practical terms, we are only pulled down by gravity immediately below us as long as we move on the ground, and it is only when we move up and away from the planet that an ever increasing part of the earth’s surface takes part in the overall gravitational pull.
Conclusion
Having used nothing but simple geometry in our analysis of the Electric Universe model of gravity, we have successfully shown that Peter Woodhead’s theory regarding an expanding earth holds against objections related to Newton’s Shell theorem as well as objections related to presumed pressures at the center of our planet.
Furthermore, we have shown that the change in surface gravity due to expansion has been about 500 per cent.
And finally, we have shown that the slow tapering of gravity for an observer moving away from the surface of our planet can be explained entirely by gravitational fields fanning out once they leave the hard crust of our planet.
In short, we can confidently state the following:
- Newton’s Shell theorem does not apply to the Electric Universe model
- The Electric Universe model allows for a hollow earth, and does in fact predict this to be the case
- Surface gravity has increased by 500 per cent from pre-expansion times without any change to our planet’s overall mass
- Gravitational fields fan out in such a way that an observer 10 km above ground experiences significant gravitational pull from locations 50 km to either side, while an observer at the ground is only pulled down by an area with a radius significantly less than five meters
Useful Links
For those unfamiliar with Peter Woodhead’s work, these are his two papers:
The following two links provide in depth information on the Electric Universe Model of Gravity and Newton’s Shell Theorem:

