By Fredrik Nygaard, 16 Feb 2016, Porto Portugal.
Also see Fredrik’s Websiite: www.universeofpartic…
Introduction
While most people are familiar with Newton’s Universal Law of Gravity and have heard about Einstein’s Theory of Relativity, with its implications on gravity, few people are aware of the existence of a third theory promoted by the Electrical Universe community, a fringe science group popular on the internet. And even fewer are aware of the basic premises and maths associated with the Electric Universe theory.
As for myself, I had not given the Electric Universe model much thought until I got involved in helping Mr. Peter Woodhead find theoretical support for his theory about the expanding earth and how the dinosaurs grew to be as large as they were.
Unlike other theories attempting to explain the impossible size of the dinosaurs, Peter Woodhead’s theory does not include any mysterious mechanism for mass increase. Instead, his theory suggests that our planet has expanded due to internal pressures and that the subsequent change in the distribution of mass has resulted in an increased surface gravity.
However, while this simple explanation solves a number of problems, Peter Woodhead’s theory got criticized for being incompatible with Newton’s Shell Theorem, which states that gravity of planets can always be modelled as point sources at their geometrical centres.
But seeing that the alternatives to Woodhead’s theory were to introduce magical mechanisms for mass creation, I found his theory deserving a closer look anyway, and it was during this investigation that it struck me that the dipole model promoted by the Electric Universe would render Newton’s Shell Theorem irrelevant.
Newton’s Shell Theorem applies to point sources only, so a dipole model of gravity would null any objections to Peter Woodhead’s theory based on this theorem.
Furthermore, as it turned out, the maths associated with the dipole model did not only support Peter Woodhead’s theory, but gave the numerical results that people had been looking for.
From fossil records, people like Stephen Hurrell had estimated that surface gravity must have increased by 300 to 400 per cent since life first appeared on our planet. And my calculations based on the assumption that gravity is a dipole at the atomic level yielded an increase in the 220 to 550 per cent rang.
The numerical range I arrived at perfectly encapsulated Stephen Hurrell’s estimates, and from this I concluded that both Peter Woodhead’s theory and the Electric Universe model of gravity are likely to be correct.
Encouraged by this, I published a paper called "The Electric Universe Model of Gravity and the Expanding Earth", now replaced by a new version called "The Dipole Model of Gravity and the Expanding Earth". And seeing that there has been little theoretical work associated with the Electrical Universe model, I decided to make a more general analysis in the hope of finding additional support for it.
The Dipole Model of Gravity
The dipole model of gravity has at its core the following characteristics from which I arrived at my findings in my first paper in support of Mr. Woodhead’s theory. And we will now use this same list of characteristics to address the problem of universal gravity and planetary orbits.
The three characteristics of dipole gravity are:
1. Gravity is a dipole at the atomic level, meaning that it has direction and polarity
2. For small bodies, such as dust, rocks and small comets, gravity atoms rotate freely to align with the dominant field
3. For large bodies, such as moons, planets and stars, gravity atoms align in such a way that their "positive poles" all point to the centre of the body, while the "negative poles" point out towards the surface
In particular, we will address the problem of planetary orbits head on, because the final point of the above list seems to suggest that large bodies will repel each other, something that is clearly not the case. So, unless we find at least one plausible explanation for planetary orbits, the dipole theory of gravity will remain suspect.
As it happens, there are at least four ways to approach this problem.
For one, we can simply note that the nucleus of chemical atoms are made up of mutually repelling protons and neutrons, yet held together anyway. In particle physics, this fundamental force is called the Strong Force, and it works through an interchange of so called Gluon particles.
If Gluon particles can overcome the enormous repelling forces inside the nuclei of chemical atoms, it seems quite reasonable to suggest that the yet to be discovered Graviton particle, supposedly responsible for gravity, can act in a similar way to hold planets in their orbits.
Another approach is to suggest that both the outside and the inside of planets are in fact involved in universal gravity, and that the round shape of stellar bodies result in a an overall attracting force.
And this is the approach we will take in this paper.
However, there is yet another approach to the problem, in which the electromagnetic properties of space result in a tethering and flux between stellar objects. This approach has quite a lot going for it too, and will be presented in an upcoming paper.
And then there’s always the possibility that gravity is not a universal force, that gravity is a local force, and that stellar orbits are in fact entirely electromagnetic, as first suggested by Johannes Kepler way back in the early 17thcentury.
For now, though, we will limit ourselves to the second approach in which the inside of stellar bodies are included in the overall gravitational force.
Stellar and Cosmic Bodies
In our analysis we will refer to large spherical bodies such as our sun, planet and moon as stellar bodies, while smaller bodies such as dust, rocks and asteroids will be referred to as cosmic bodies.
And since we will find in our analysis that the two types of bodies do not behave identically in a dipole universe, the distinction is not merely cosmetic but mathematically significant. The reason for this is that stellar bodies have "negatively charged" external surfaces, while cosmic bodies have freely rotating dipoles.
Furthermore, in my paper "The Dipole Model of Gravity and the Expanding Earth", I showed that dipole gravity implies that all stellar bodies have a "positively charged" internal surfaces, and we will use this as a fact in this paper.
We will define stellar bodies as having a "negatively charged" outer surface and a "positively charged" inner surface, and we will define cosmic bodies as having freely rotating dipoles.
Only under extreme circumstances will a stellar body allow its dipoles to change their orientation, in which case the stellar body ceases to be a stellar body, and becomes a cosmic body instead. Intermediate size bodies like asteroids and small comets may flip flop between being a stellar and a cosmic body depending on the size and proximity of the objects it interacts with.
Repelling and Attracting Surfaces
Taking the earth and the moon as an example we have the following repelling and attracting surface combination:
1. Outer surface of moon repels outer surface of earth
2. Inner surface of moon repels inner surface of earth
3. Outer surface of moon attracts inner surface of earth
4. Inner surface of moon attracts outer surface of earth
Furthermore, we have to consider the shape of the surfaces involved since it is reasonable to expect that this will have an effect on how gravity spreads through space.
Since we are dealing with dipoles, we can assume that only surfaces facing each other are interacting with each other. The back of the moon, for instance, does not interact with our planet, nor does the back of our planet, as seen from the moon, interact with the moon.
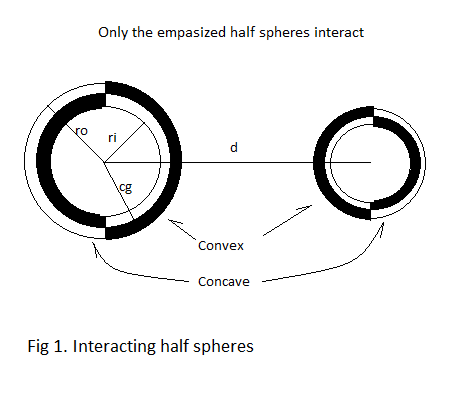
And from this we see that we have repulsion between the two convex outer surfaces and between the two concave inner surfaces, while the two convex-concave pairs attract each other.
From this again, it follows that we have the following factors to consider:
1. The shape of the surface, being either Convex or Concave
2. The radius "ro" from the geometrical centre to the outer surface
3. The radius "ri" from the geometrical centre to the inner surface
4. The radius "cg" from the geometrical centre to the centre of gravity
5. The distance "d" between the geometric centres of the two bodies involved
And from this again, we can produce the following two functions:
· Convex(ro, ri, cg, d)
· Concave(ro, ri, cg, d)
These two functions describe the moderating factors that apply to Newton’s Universal Law of Gravity, which we will use as our base function.
For example, the force between the two outer surfaces of a pair of stellar bodies, M1 and M2, can now be expressed as:
F = – Convex(ro1, ri1, cg1, d) * Convex(ro2, ri2, cg2, d) * G*M1M2/d^2
The geometry of the two stellar bodies has now been added to our base function in the form of two moderating functions.
To simplify things, we can use the fact that the geometries expressed by the Concave and Convex functions are related to the two bodies M1 and M2, and we can therefore use Convex(1) as shorthand for Convex(ro1, ri1, cg1, d) and Convex(2) as shorthand for Convex(ro2, ri2, cg2, d). And if we simplify things further by expressing our base function as B(d) instead of G*M1M2/d^2 we get the following shorthand for the above function:
F = – Convex(1)*Convex(2)*B(d)
Note that we have made the force negative in this particular case since the two convex surfaces are both "negatively charged", and therefore repelling each other.
Note also that we are not saying anything about what the moderating functions do. We are simply saying that they play a role in determining the force between stellar bodies. However, we can make the assumption that the Convex function will result in a force that tapers off quicker than a force moderated by the Concave function.
Concave surfaces are after all generally associated with focus, while convex surfaces are associated with spread. A satellite dish is a typical example of a focusing device based on the geometry of a concave surface, while lamps designed to spread light in all directions use convex surfaces to do this.
Deriving the Universal Gravity Function for Stellar Bodies
Armed with Newton’s Universal Law as our base function and the Convex and Concave functions as moderating factors, we are now in a position to derive a function for gravitational force between two stellar bodies.
Using our shorthand notation we get the following four equations for the four surface combinations of two stellar bodies:
1. The two convex outer surfaces repel each other according to
F = Convex(1)*Convex(2)*B(d)
2. The two concave inner surfaces repel each other according to
F = Concave(1)*Concave(2)*B(d)
3. The first concave-convex surface combinations attracts each other according to
F = Concave(1)*Convex(2)*B(d)
4. The second concave-convex surface combinations attracts each other according to
F = Convex(1)*Concave(2)*B(d)
Subtracting the repelling forces from the attracting forces we get the overall force:
F = Concave(1)*Convex(2)*B(d) + Convex(1)*Concave(2)*B(d)
– Convex(1)*Convex(2)*B(d) – Concave(1)*Concave(2)*B(d)
F = (Concave(1)*Convex(2) + Convex(1)*Concave(2)
-Convex(1)*Convex(2) – Concave(1)*Concave(2)) * B(d)
And from this we see that we have a complex geometrical expression that is rather lengthy to write. If we give this lengthy expression the shorthand notation Complex() we can express the full equation as:
F = Complex() * B(d)
where
Complex() = Concave(1)*Convex(2) + Convex(1)*Concave(2)
– Convex(1)*Convex(2) – Concave(1)*Concave(2)
B(d) = G*M1M2/d^2
Analysing the Universal Gravity Function for Stellar Bodies
Note that while the base function is known to us as B(d) = G*M1M2/d^2, we do not have any specific knowledge of the Concave and Convex functions apart from our assumption that the Concave function moderates the base function in a more focusing manner than the Convex function.
The surface combinations have the theoretical capability of moderating the base function in such a way that we get a Newtonian result for a large range of values. And this is in fact how things must be in order to conform with observations.
With Newton’s Law agreeing well with a wide range of observations, our full function must give results that agree with Newton’s Law for the distances where Newton’s Law can be applied without moderation.
However, this is not to say that our full function will agree with Newton for all values. At extremely short distances for instance, the two outer surfaces of a stellar combination will dominate the complex geometry.
The two outer surfaces are the only ones that can have direct contact with each other, which means that these mutually repelling surfaces have the potential to generate enormous repelling forces, easily dwarfing all the other geometrical factors.
As a result, our universal function is likely to reduce to the following for extremely short distances:
F = – Convex(1)*Convex(2)*B(d)
And observations do in fact confirm this. Binary stars in extremely close orbit with each other are tremendously unstable and will either merge into a single object or definitely repel each other into a wider and more stable orbit within months, a mere blink of an eye in the cosmic scale of things.
The two outcomes of a very close encounter between stellar objects is in other words a swift repulsion or a merger, exactly as predicted by our investigations so far.
As for very large distances there is another interesting prediction we can make from our function. Since the concave-concave combination is the one with the greatest degree of focus, this part of the overall function will become dominant at some point even if it is relatively insignificant at shorter distances.
At large distances our universal function reduces to:
F = – Concave(1)*Concave(2)*B(d)
Again we are getting a repelling force.
And this too is in accordance with observations. Distant galaxies are not only receding from each other, but are accelerating rather than slowing down. Something is pushing distant galaxies apart, and with no good explanation for this in the standard model, the repelling force is put down to a mysterious "dark energy".
However, using our function, we see that the observed repulsion is in fact what we would expect. This phenomenon that cannot be satisfactorily explained in the standard model is nothing more than gravity itself, acting as a repelling force at large distances.
Establishing the Newtonian Range for Stellar Bodies
At this point we have found that our universal function for stellar bodies yields a repelling force at extremely short distances and also at large distances, and it follows from this that there must be two zero points where gravity goes from negative to positive. One of these zero points exists at an extremely short distance, and the other one exists at a very large distance.
A consequence of this is that there is an upper and a lower limit to the size of stellar orbits. And since all of this is dependent on the geometry of the bodies involved we can assume that a large stellar body can support a wider orbit than a smaller stellar body even if the mass of the two bodies are the same.
For our sun, we know that its stellar companion with the widest known orbit is the dwarf planet Eris which at its most distant is about 100 astronomic units away from the sun. So we know the distant zero point has to be farther away than this, but not necessarily much farther away.
The near zero point for stellar bodies orbiting our sun must by the same logic be closer than the orbit of Mercury, but not necessarily all that much closer. Mercury does after all exhibit non-Newtonian behaviour in its orbit, which indicates that it is in an area close to where gravity starts changing from an attracting to a repelling force.
From observations it would appear that the Newtonian range for our sun relative to its planets is located in the Mercury to Eris range, and that any stellar body outside this range will display non-Newtonian behaviour.
For bodies larger than the sun, the Newtonian range can be expected to be at a greater distance both to the inside and to the outside, while smaller bodies will have its Newtonian range at a shorter distance.
This follows from the general logic of geometry, where things can be expected to behave in a proportional manner. But we also have observational evidence to support this assumption.
Mercury is after all in a slightly non-Newtonian orbit around the sun, while our moon is distinctly Newtonian in its orbit around our planet, despite being much closer to the earth than Mercury is to the sun.
The relatively small size of our planet compared to the sun is clearly of importance when comparing the two orbits.
Plotting the Universal Function for Stellar Bodies
To sum things up, we now know from theory and observation that our universal function for stellar bodies has to conform to Newton’s Law for distances typical in our solar system, but turn negative for extremely short distances and very large distances, and from this we are in a position to plot the following graph of force against distance:
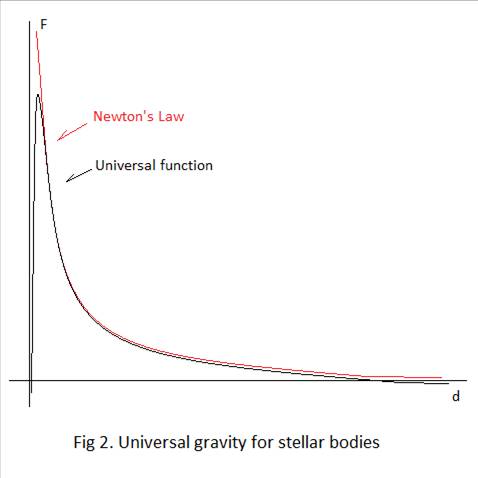
The curve of our universal function is smooth and natural, and without knowing much more than this at the moment, we can so far conclude that the Complex function should be relatively easy to derive.
Given enough data points it should be possible to derive both the Concave and the Convex function.
Gravitational Capture and Stability
Finally, before going on to discuss cosmic bodies, it should be noted that the fact that gravity becomes repelling between stellar bodies at extremely short distances, yet positive at intermediate distances, means that this Universal Gravity function based on the dipole model has in it the mechanism required for a stellar body to capture another body and subsequently stabilize its orbit.
In general, we can say that the dipole model produces a more stable universe with stellar bodies rarely being pulled out of one system without being included in another. In a collision scenario with two solar systems coming into close contact, there will be tremendous upsets, but things will stabilize relatively quickly.
Capture and a quick return to stability will be the rule in a dipole universe, rather than the chaos of collisions and scatter predicted by the point source model.
Universal Gravity applied to Cosmic Bodies
While the stellar bodies that we have discussed so far can be thought of as spherical shells with a "negatively charged" outer surface and a "positively charged" inner surface, cosmic bodies can best be described as bodies containing freely rotating dipoles.
And it follows from this that the biggest difference between a stellar body and a cosmic body, apart from their different size, is that the dipoles of a cosmic body will always orient themselves in such a way that there will be attraction between them and whatever other body they are influenced by.
Furthermore, cosmic bodies have no "charged surfaces", and it follows that our universal function for stellar bodies cannot be used for cosmic bodies.
A cosmic body in gravitational interaction with a stellar body will be under influence of the two surfaces of the stellar body, and the dipoles of the cosmic body will orient themselves towards whichever surface is the dominant one.
At short distances, the outer surface will dominate. However, due to the moderating effect of curvature, the internal surface will dominate beyond a zero net gravity point as illustrated in Fig 3.
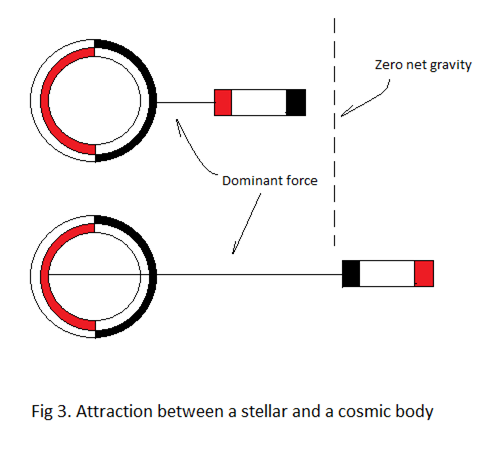
The existence of a zero net gravity point follows from the fact that there can be no net gravity where the dipoles of the cosmic body turn to realign themselves with a different surface of a stellar body.
Paradoxically, gravity will taper off to zero and then grow again for a while before again tapering off towards zero, and it follows from this that there must be a region around every stellar body which is virtually free of any cosmic bodies, yet where there is a marked increase in the density of such bodies at a farther distance.
This follows from the fact that nothing can form a stable orbit at zero gravity. Any motion in such a region will cause a cosmic body to either fly off into a farther region or plunge closer to the stellar body.
Mathematically we no longer have four, but two curved surfaces to consider, and we have to allow for the fact that cosmic bodies always let their dipoles align in such a way that they attract.
From this we get:
F = | Convex(1)*B(d) – Concave(1)*B(d) |
F = | Convex(1) – Concave(1) | * B(d)
In other words, we have the same base function B(d) = G*M1M2/d^2, but a different moderating geometry. And we express the fact that this function never goes negative with the use of absolute value symbols.
Furthermore, we can simplify the above by using the shorthand name Combined() to express the moderating term:
Combined() = | Convex(1) – Concave(1) |
And we can write our universal function as follows:
F = Combined() * B(d)
where
Combined() = | Convex(1) – Concave(1) |
B(d) = G*M1M2/d^2
Analysing the Universal Function for Cosmic Bodies in Interaction with Stellar Bodies
The difference between the universal function for two stellar bodies and for a cosmic body interacting with a stellar body is confined to geometry. The base function B(d) is the same in both cases. However, the Complex and the Combined functions are very different, and we must therefore expect significant differences between the two cases, at least in certain regions.
However, one thing the two universal functions must have in common is an ability to be Newtonian for a large range of values. Just like the Complex function must produce a linear result for the Newtonian range, so must the Combined function.
However, this is not to say that the Newtonian range for cosmic bodies is the same as that of stellar bodies. In fact, it is easy to see from the geometrical functions themselves that this cannot be the case. They are much too different to result in identical Newtonian ranges.
One big difference between the functions is that the Complex function has two zero points, beyond which there is negative gravity while the Combined function has a single zero point in between two positive regions.
There is no negative solution for the Combined case, and it follows that there is no limit to where cosmic bodies can orbit relative to a stellar body.
With the notable exception of the zero point, cosmic bodies can establish stable orbits at any distance around a stellar body.
Orbital Speeds
An important consequence that can be derived from the fact that the Complex and Combined functions are different is that stellar and cosmic bodies will not generally orbit a stellar body at the exact same speed. In most regions, there will be a difference in speed between these two types of bodies, and as a consequence, the larger stellar body will gobble up all the smaller cosmic bodies that constantly get in its way.
However, since the Combined function has a different shape than the Complex function, there may be one or more region where stellar bodies orbit at pretty much the exact same speed as cosmic bodies.
In such regions, we would expect to find a high density of asteroids together with one or more stellar body. And as a matter of fact, we have two such regions in our solar system. The closest being the Asteroid Belt with its dwarf planet Ceres, and the more distant being the Kuiper Belt with its dwarf planet Pluto.
This suggests that there are two points where the Complex and Combined functions yield identical values:
Complex() = Combined()
Complex() = | Convex(1) – Concave(1) |
Assuming the two solutions are at either side of the zero point for the combined function, we get the following two solutions:
Complex() = Convex(1) – Concave(1) { for the near solution }
and:
Complex() = Concave(1) – Convex(1) { for the far solution }
And since this is a general observation that we must assume to be true for other solar systems too, we can make the prediction that most, if not all solar systems, possess two asteroid rich regions corresponding to our Asteroid Belt and Kuiper Belt.
Plotting the Universal Function for Cosmic Bodies Orbiting Stellar Bodies
From the above analysis, we can now plot the graph for the universal function for cosmic bodies orbiting stellar bodies. And by superimposing the graph for two stellar bodies interacting with each other, as well as Newton’s Universal Law, we get the following:
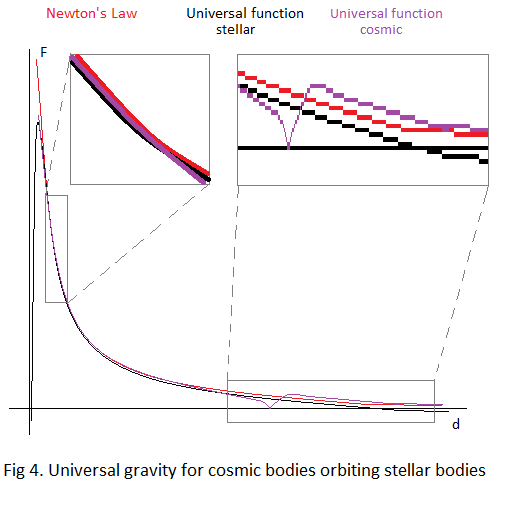
As we can see, the far point where the Complex and Combined functions are equal is relatively easy to spot, while the near solution is less obvious. And it follows from this that there should be observable anomalies in the far region, while any anomaly in the near region would be almost undetectable.
It is also clear that we now have even more data points that we can use in order to derive the Concave and the Convex functions.
The more anomalies we can find, the more data we have, and with the far region of our solar system being a likely place to find anomalies for cosmic bodies, we proceed to look into the known anomalies for that region before looking into anomalies and interesting observations closer to home.
Orbits of Long-Period Comets
The orbits of long-period comets have always posed a problem for astronomers. Comets that travel beyond the Kuiper Belt all have orbits that have proven themselves impossible to predict, and many do not return at all.
This anomaly has been put down to gravitational pull of nearby stars and the hypothetical existence of an asteroid rich region in deep space called the Oort Cloud. However, as we will see, no Oort Cloud is needed to explain the observed facts.
The fact that many comets do not return is most probably due to the fact that most comets are intermediate size bodies, and such bodies will typically be expelled from our solar system once they go beyond the point where gravity for stellar bodies goes from being an attracting to a repelling force.
And with comets also being small enough to display cosmic body properties, they will be affected by the zero point for cosmic bodies. As seen from a standard model viewpoint, comets travelling away from our sun will first be subjected to an unexpectedly small gravitational pull before being subjected to an unexpectedly large pull.
Orbits of long-period comets cannot be predicted by the point source model because their orbits are not perfectly elliptical. And from this it follows that the hypothetical Oort Cloud is unlikely to exist since the basis for its proposed existence no longer holds.
The Pioneer Anomaly
After passing about 20 AU from the sun, the deep space probes Pioneer 10 and Pioneer 11 no longer followed the path predicted by the standard model. Instead, the deep space probes followed a path conforming to a slightly stronger than expected gravitational pull towards the sun.
The accepted explanation for the anomaly is currently put down to a phenomenon called thermal recoil force, where it is suggested that heat escaping through the shady side of the probes exert a force towards the sun. However, this rather fanciful explanation is only required for the standard model since the phenomenon can easily be explained as dipole gravity.
On their way out of the solar system, the deep space probes first entered a short region with low gravitational pull towards the sun before entering a large region with gravity higher than standard theory predicts, and while the effect of the first region went undetected, the effect of the subsequent higher than expected gravity region became so evident that it could not be put down to measurement errors.
Interestingly enough, the anomaly was first discovered at 20 AU which is at the start of the Kuiper Belt. And since we have already established that the zero point for cosmic bodies orbiting the sun is located between the Asteroid Belt and the Kuiper Belt, the location of the anomaly fits our theory very well.
The Kuiper Belt is at the trailing end of the region where dipole gravity for cosmic bodies is stronger than standard theory predicts. And it follows that the Kuiper Belt is where we would expect to detect an anomaly of this sort.
The short distance with low to no gravity was passed undetected, and it was not until the space probes were well into the region of stronger gravity that the anomaly was detected. But this is no surprise since no one expected to see any anomaly at all. The relatively short region of low gravity did evidently not produce a large enough deviation to catch the attention of astronomers.
However, the anomaly should not have come as a complete surprise. Comets follow the same general path as the deep space probes, and we have known for a long time that comets do not follow perfect elliptical paths, so why should we expect the deep space probes to somehow behave differently?
Flyby Anomalies
Closer to home, we have the so called flyby anomalies, which are marked by an unaccounted for velocity increase for space probes using our planet’s gravitational field to accelerate.
As a matter of fact, all sorts of near surface anomalies have been known to scientists for a long time, so the flyby anomaly should not have come as a big surprise. Close to the surface of our planet, things do not generally conform well with the point source model. The flyby anomalies are in other words just one of many anomalies associated with near surface gravity.
As for our dipole gravity model, these anomalies contain important clues to the nature of the Convex function, because the effect of Earth’s internal surface can be ignored when modelling near surface phenomenons.
Very close to Earth our function
F = | Convex(1) – Concave(1) | * B(d)
can be reduced to
F = Convex(1) * B(d)
And from my paper "The Dipole Model of Gravity and the Expanding Earth", we have that only a part of our planet’s mass is involved in pulling on an observer in close proximity of our planet.
Furthermore, the amount of matter involved in pulling on an observer increases with altitude, not in a linear manner, but in a non-linear manner depending on the radius of our planet and the thickness of our planet’s non-gaseous shell.
Generally, gravity tapers off at a slightly more rapid rate for dipole gravity than the point source model predicts. However, at distances where the mass of our planet is getting increasingly involved at an above average rate, the gravitational force predicted by the dipole gravity model may well exceed what is predicted by a point source model.
And since flyby anomalies display an excess in force, we can conclude from the dipole perspective that these flybys occur at altitudes where dipole gravity is relatively stronger than the point source model predicts.
For relatively low altitudes, the Convex function is identical to the moderating function of mass described at length in my paper on the expanding earth. Presumably, the moderating function discussed in the expanding earth paper is identical to the Convex function proposed here.
The Role of Interstellar Dust in Galaxies
Having considered cosmic bodies orbiting our sun and the Earth, we can go on to consider cosmic bodies under the influence of more than one stellar body, as is the case for interstellar dust and rocks.
Under such circumstances, the dipoles of cosmic bodies will always align themselves with the dominant field. However, if at all possible the dipoles will align themselves so as to attract all the fields influencing them, and not only the dominant one.
The dipoles will always seek to orient themselves in such a way that they produce a maximum net attracting force. And the result of this is that interstellar dust and rocks play an important role in countering the repelling forces between stellar bodies.
While stellar bodies repel each other at large distances, cosmic dust and rocks have the effect of producing a net attracting force between stellar objects. And the more dust and rocks there is in a region separating two stellar bodies, the more net attraction there will be.
Given the right relative proportions of cosmic and stellar bodies we end up with a stable system that keeps its shape in the typical non-Newtonian way that galaxies do.
Had this not been the case, our Milky Way Galaxy, with its diameter of about 120 000 light years, would have been completely blown apart by the repelling forces between stellar bodies. But as is evident from observation, the Milky Way Galaxy holds itself together nicely.
The dusty arms of our spiral galaxy are like ropes spinning out from its dusty centre, and the mutually repelling forces between the spinning arms keep the structure in place. The arms are held together by the attracting forces of dust and rocks, while the repelling forces acting through the relatively dust and rock free space between the arms keep them from blending into each other.
Again we have found an explanation for something that is not easily explained by the standard model. The rope-like structure of spiral galaxies defies the standard model, and the concept of "dark matter" has been introduced to make the theory fit observations. However, given the right properties for the Concave and Convex functions, and keeping in mind that stellar bodies are hollow, and therefore much less massive than generally assumed, there is no need for dark matter. The stable nature of galaxies may well be fully accounted for by a further analysis of the maths associated with dipole gravity.
As for the largely dust free space between galaxies, there is nothing to counter the repelling forces, and we have repulsion winning out, pushing galaxies apart.
Gravity Between Cosmic Bodies
Having dealt with stellar bodies interacting with each other, and stellar bodies interacting with cosmic bodies, we can move on to cosmic bodies acting on each other. And as an example of two such bodies we can take the case of a satellite visiting a small comet, and we will see that the measured gravity between these two objects will be very different from what would be anticipated from the standard model.
Consisting entirely of freely rotating dipoles, cosmic bodies do not have any moderating functions associated with them and we can conclude that the force acting between two cosmic bodies are defined entirely by Newton’s Universal Law.
However, with very little coordination among each other, the dipoles will produce an overall pull that is much less than the mass of the objects would suggest, and this serves to explain why the standard model predicts comets to be dirty snowballs when in fact they are made of rock.
The low gravitational field of a comet is not due to a lack of mass, it is due to the dipole nature of gravity and the lack of coordination between gravity atoms for relatively small bodies.
Black Holes
At this point it is clear that we do not have any need for dark energy or dark matter when we use the dipole model of gravity. Both phenomenons are inventions made up in order to make the standard model work.
And by definition, black holes have to go too, since there is no such thing as a point source of gravity in the dipole model. Dipoles cannot line up in such a way that they generate a single point of gravitational pull.
Furthermore, dipole gravity, either on its own or in combination with electrical forces and plasma, can solve all the problems that black holes were meant to solve, completely removing the theoretical need for their existence.
The Big Bang
The Big Bang is another invention that seeks to remedy the shortfalls of the standard model, and its purpose is similar to that of dark energy.
Seeing that galaxies recede from each other, there was a need to explain this, and the Big Bang theory was adopted to do that. However, galaxies recede from each other due to the repelling forces of gravity at great distances, so the Big Bang has no purpose in a dipole universe.
Furthermore, there is no need for a beginning or an end to the universe where there is a balanced equilibrium between repelling and attracting forces, and the dipole model is capable of providing such a balance, so the whole idea of a Big Bang is no longer needed.
Instead of a Big Bang we can propose a perpetual mechanism where large bodies come into existence through the assembly of smaller parts, and that these large bodies subsequently expend themselves through radiation and outflow of matter which in turn provides building material for a new generation of large bodies, starting the cycle over again.
Such a universe has no beginning and no end, only creation and destruction.
Anti-Gravity
On a final note, we see that dipole gravity has in it the elements required for anti-gravity. In fact, we have already concluded that anti-gravity exists between stellar bodies at large and extremely short distances. Gravity that exerts a repelling force is after all the definition of anti-gravity.
However, to produce an anti-gravity device to be used in a flying machine we will somehow have to trick nature. Cosmic bodies will always attract other bodies since their dipoles always align with the dominant gravitational field, and it is only by somehow interfering in this alignment process that an anti-gravity device can be constructed.
But there is no reason to believe that it is impossible to construct a device to manipulate the dipoles of matter, so we have no reason to believe that anti-gravity devices cannot be made. And we must therefore conclude that the construction of an anti-gravity device is a theoretical possibility that may one day be turned into reality.
Conclusion
Having made the assumption that gravity is a dipole, and that gravity is a force that acts unhindered through matter, we arrived at the following set of conclusions:
1. Stellar bodies repel each other at large distances
2. "Dark energy" is gravity acting in a repelling manner between stellar bodies at great distance
3. Stellar bodies repel each other at very close distances, preventing them from colliding
4. There is a maximum and a minimum size to stellar orbits depending on the size of the orbiting bodies
5. Mercury’s non-Newtonian behaviour is due to it being close to the inner limit of allowed orbits around the sun
6. There is a region of zero net gravity for dust and rocks located somewhere between the Asteroid Belt and the Kuiper Belt
7. Dust and rocks do not generally orbit the Sun at the same rate as planets
8. The Kuiper belt and the Asteroid belt are the only two regions where dust and rocks orbit the sun at the same speed as planets
9. Other solar systems are likely to possess two asteroid rich regions, just like our own solar system
10. Comets do not follow perfect ecliptic paths
11. The "Oort Cloud" does not exist
12. The Pioneer anomaly is due to non-Newtonian gravity effects beyond the Asteroid Belt
13. Flyby anomalies are due to non-Newtonian gravity effects close to stellar bodies
14. "Dark matter" is dust and rocks acting as glue to hold galaxies together
15. Comets are more massive than standard theory predicts
16. "Black holes" do not exist
17. Cosmos is infinite in time and there was no "Big Bang"
18. Anti-gravity devices are theoretical possibilities
Useful Links
Peter Woodhead’s theory of a mechanism for an expanding earth:
My essay on dipole gravity and the expanding earth: www.checktheevidence…
Wallace Thornhill presenting Ralph Sansbury’s dipole gravity model:
Stephen Hurrell’s book on dinosaurs and the expanding earth:
Fundamental forces of nature:

