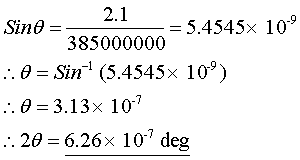Revised 14.10.2005 following Corrections from Dean Rose (thanks!) – though the conclusion seems to be the same
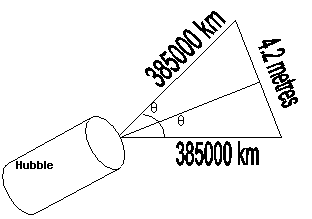
To try to answer this question, we need to know the distance from the Earth to the Moon and the width of the Lunar Module. In the approximate calculations I have made below, I have assumed the width/diameter of the LEM to be 4.2 metres (www.nationmaster.com…) and the distance from the Earth to the Moon to be 385000 km. So, with some simple trigonometry, we can work out the apparent width (in degrees) of the Lunar Module as seen from Earth. Hubble’s quoted resolution seems to be quoted as “better than 0.1 seconds of Arc” (www.stsci.edu/hst/HS…), 0.05 seconds of Arc (dept.physics.upenn.e…), 0.014 seconds of Arc (hyperphysics.phy-ast…)
|
|
(Call this A) |
Hubble’s resolving power is quoted at 0.05 seconds hence the resolving angle in degrees is:
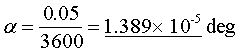 (Call this B)
(Call this B)
If Hubble’s resolution is as fine as 0.014 seconds of arc then the resolving angle in degrees is:
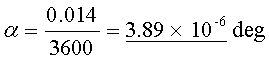 (Call this C)
(Call this C)
I would therefore agree that, according to published figures, the angle subtended by the 2 opposite sides of the Lunar Module is approximately 22 times (resolution 0.05) too small (B/A), or 6.2 (C/A) times too small (resolution 0.014), according to the above calculations, for Hubble to see the Apollo Craft on the Moon. That is:
NO, HUBBLE CAN’T SEE APOLLO CRAFT ON THE MOON
THEY ARE JUST TOO SMALL…